무한한 심해 탐험
[21년 1월 2주차] 생성 모델, 어떻게 평가해야 할까? (EPFL 유재준) 본문
생성모델을 어떻게 평가할 것인가?
Evaluating Generative Models Correctly : Density and Coverage
Summary
- -> Fidelity와 Diversity Metrics는 평가 수단으로서 매우 유용하다.
- -> Precision과 Recall은 문제점을 가지고 있다.
- -> Density와 Coverage는 이러한 문제점을 해결할 수 있다.
- -> CNN 구조의 Random Embedding을 적용하게 되면 좀더 General한 어플리케이션이 가능하다.
Outlier가 있어도 evaluation 모델이 영향을 받지 않게 하도록 만드는 것이다!
생성 결과물을 어떻게 평가할 것인가? 생성모델에 열광하는 이유는 무엇인가? 학습기반 모델은 대개 Discriminative 모델과 Generative 모델 총 두가지로 나뉜다. 두 모델은 문제를 접근 하는 방식이 둘다 다르다.
Discriminative Model
분류문제 혹은 지도 학습 문제 해결 방식은 Discriminative 모델이 주로 이용된다. 데이터 사이의 경계선을 택하는 방식으로 알고리즘 개발이 쉽고 성능이 쉽다. 판별 모델링으로도 불리며, label Y가 필요하다.
Generative Model
생성 모델의 경우, 데이터 분포를 학습하는 간접적인 방식이 많다. 경계선을 배우는게 아니다. 성공하다면 분류 등 다양한 분야에도 사용된다. 생성 모델은 데이터 생성을 확률적 모델의 방식으로 생성하며 모델에서 샘플링하는 방식을 통해 새로운 데이터를 생성할 수 있다. 생성모델은 주로 unsupervised learning 이며 label Y가 필요없다. (label Y가 필요한 경우도 있음 = 뭘까요?)
베이지안 트뤠인? (MAP) Maximum a Posteriori
주어진 Data가 반영된 W가 가장 잘 설명될수 있는 W를 구하는 것. MLE에 비해 W에 대한 Prior만 추가된 형식이다.
taeoh-kim.github.io/blog/bayesian1/
모든 이미지의 recovering 방식은 이와 같은 수식으로 표현이 가능하다.
생성모델의 priority를 잘 얻으면 강력한 생성모델을 얻게 되며, 이는 다양한 연구분야에 같은 프레임워크로 적용할 수 있게 된다.
생성모델은 특성상 평가를 하는 것 자체가 애매하다!
평가를 할 수 있는 기준이 없다보니 휴리스틱(heuristics)한 방식으로 접근하게 된다.
그러나 사람이 평가하는 것은 괜찮은가?
이미지를 사람이 평가할 경우,
(1) 일일이 평가를 해야 하는 것이기 때문에 평가하는 속도는 느리다.
(2) 사람마다 기준도 다르고, 동일한 사람의 시간적인 평가도 다르기 때문에 정량화가 어렵고 재현이 불가능하다.
(3) 또한, 의료 분야 등 제한된 분야에 대해서 평가할 수 있는 사람에 따라서 다르고 오감에 따라서도 다르다. (시각, 청각 등)
(4) 또한, Mode-collapse 현상을 잡아내지 못한다.
여기서 Mode란?
데이터 분포에서 Mode란 관측치가 높은 부분을 의미한다. 정규분포에서는 평균이 분포의 mode이다.
single = mode 1개
bimodal = mode 2개
multimodal / multiple modes = mode 2개 이상
ex. MNIST dataset의 경우, 총 10개의 multiple modes 분포이다.

-> BCE Loss의 문제점이기도 한데, 생성자가 다양한 이미지를 만들어내지 못하고 비슷한 이미지만 계속해서 생성하는 경우를 뜻한다. 이는 생성자가 판별자를 속이는 적은 수의 샘플을 찾을 때 발생한다. 따라서 한정된 이 샘플 이외에는 다른 샘플을 생성하지 못하면서, 생성자가 local minimum에 빠지게 된다. (왜죠?)
도메인이 많아질 경우, mode-collapse가 늘어났나요..?를 잡아내지 못한다. 퀄리티에서는 예민하지만 (진짜 같냐) 그러나 얼마나 다양하느냐에 대해서는 예민하지 못한다. (Diverse)
Evaluation Pipeline
- Embeddings
이미지로 예시를 들 때, 이미지와 이미지를 비교하는 것은 의미가 없다. 왜냐하면 컴퓨터가 이해하는 것은 이미지가 아닌 픽셀이기 때문인데, 픽셀간의 Shift 혹은 빼고 더하는 것은 Semantic한 의미를 담고 있기가 어렵다. 왜냐하면 그런 계산 과정에서 전혀 다른 의미(단 하나의 이동으로도 큰 값을 만들어낼 수 있음) 를 만들어 낼 수 있기 때문이다.
그러므로 embedding space가 매우 중요하다.
Embedding Space란?
embedding은 고차원 벡터의 변환을 통해 생성할 수 있는 상대적인 저차원 공간을 가리킨다. 임베딩을 사용하면 단어를 나타내는 희소 벡터와 같이 커다란 입력값에 대해 머신러닝을 더 쉽게 수행할 수 있다. 임베딩이 잘 동작하는 경우는 보통 의미가 유사한 입력값들을 임베딩 공간 안에 서로 근접하게 위치시켜 입력값의 특정 의미를 포착하는 것이다. 임베딩은 모델과 관계없이 학습과 재사용이 가능하다.
출처 : 구글 머신러닝 단기집중과정
-> representation learning 분야임. 이거를 하기 위해서는 의미 있는 곳으로 보내줄 수 있도록 representation mapping function을 배워야 한다. embedding할 샘플을 의미있는 피쳐(Feature) 공간으로 보내야 하는 embedding 과정이 필요하다.
- Building distribution
-> 한 군집단과 다른 군집단의 분포를 나타내는 방법을 고안해야 한다. 방식은 여러가지이다. 확률분포를 어떻게 만들거냐?
원을 만드는 거면 kernel density map을 사용해야하고, 가우시안 방식으로 하는 방법도 있다. 보통 쉬운 예시로는 가우시안 분포 1 mode를 주로 사용


- Quantifying the discrepancy
-> 두 분포를 만들었으면 두 분포간의 차이도 계산해야한다.
-> Divergence나 Score Matrix도 사용해볼 수 있다.
FID (Frechet Inception Distance)

FID는 확률분포의 거리를 구하는 것이다. 거리를 계산하는 것이기 때문에 값이 적을 수록 generate한 데이터들의 퀄리티가 좋다.
Inception score를 사용하지 않고 FID를 사용하는 이유?
Inception Score는 Real 데이터를 사용하지 않고 Fake 데이터만 사용하여 점수를 내게 되는데 이 때 평가기준으로 2가지가 사용된다.
* 평가기준 1 : 이미지가 의미가 있어야 한다.
* 평가기준 2 : 의미가 있으면서 다양한 이미지를 생성해야 한다.
Inception Score는 값이 클 수록 좋은 모델이다. (왜? 수식 이해 아직 안함) 그러나 실제 데이터가 어땠는지에 대해서는 계산을 하지 않기 때문에 FID가 생겼다. FID는 실제 데이터랑도 비교하는 기능이 있기 때문이다.
FID는 Inception network의 중간 레이어에서 feature를 가져와 활용한다. <- 이해가 빈약하다.
-> Embeddings : Inception feature space
-> Building distributions : Gaussian distribution
-> Quantifying the discrepancy : Frechet distance
FID가 낮을 수록 좋다~ (평균도 같고... )
FID가 사람보다 나은 점이 뭐죠?
- 비교적 사람보다 빠르다.
- 정량화 결과 재현이 가능하다.
- 이미지에 한해서는 사람보다는 광범위한 적용을 할 수 있다. (의료영상에 대해서 Fine Tuning 하는 식)
- 중간에 Feature을 갖고와서 샘플을 뽑을 수 있다.
- Mode-Collapse 현상을 어느정도 잡아냄.
생성모델이 고도화 되면서 FID의 문제점이 보이기 시작한다. 생성모델이 만들어낸 데이터들의 퀄리티를 하나의 기준값으로 평가하기에는 더 고려할 수 있는 부분이 많다. 이미지의 퀄리티는 Fidelity와 Diversity 두 가지가 있으므로 두 가지를 따로따로 봐줘야할 필요가 있다.
Less Realistic vs More Realistic
- FID는 Less 쪽이 More 보다 값이 높다.
Less Diverse vs More Diverse
- FID는 Less 쪽이 More 보다 값이 높다.
(앞서 말했듯이 FID 값이 높을 수록 이미지는 퀄리티가 떨어진다고 볼 수 있다.)
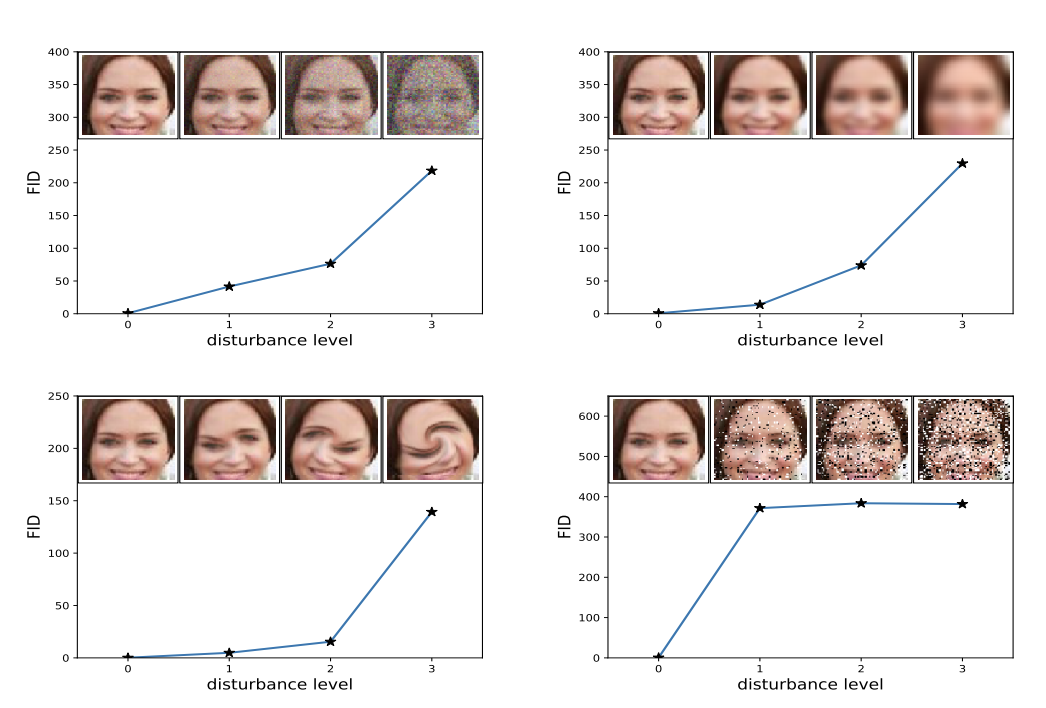
그럼 만약에 둘이 엮여있다면 어떤 모델이 더 우수한가?
Less Diverse & More Realistic vs More Diverse & Less Realistic
실제 결과값에서는 FID가 비등비등하게 나온다. 노이즈에 따라, 어떤 걸 샘플링 했느냐에 따라서 FID가 다르게 나온다. 이럴 경우에는 FID로는 모델의 세밀한 분석이 불가능해진다.
P&R (improved version)
Precision -> Fidelity
- Among Fake Samples, which proportion is Close to real?
Recall -> Diverse 재현율
- Among Real Samples, which proportion is Close to fake?
k-NN을 이용해서 "Close to" 라는 단어를 정의한다. (물론 k는 휴리스틱하게 정한다.)
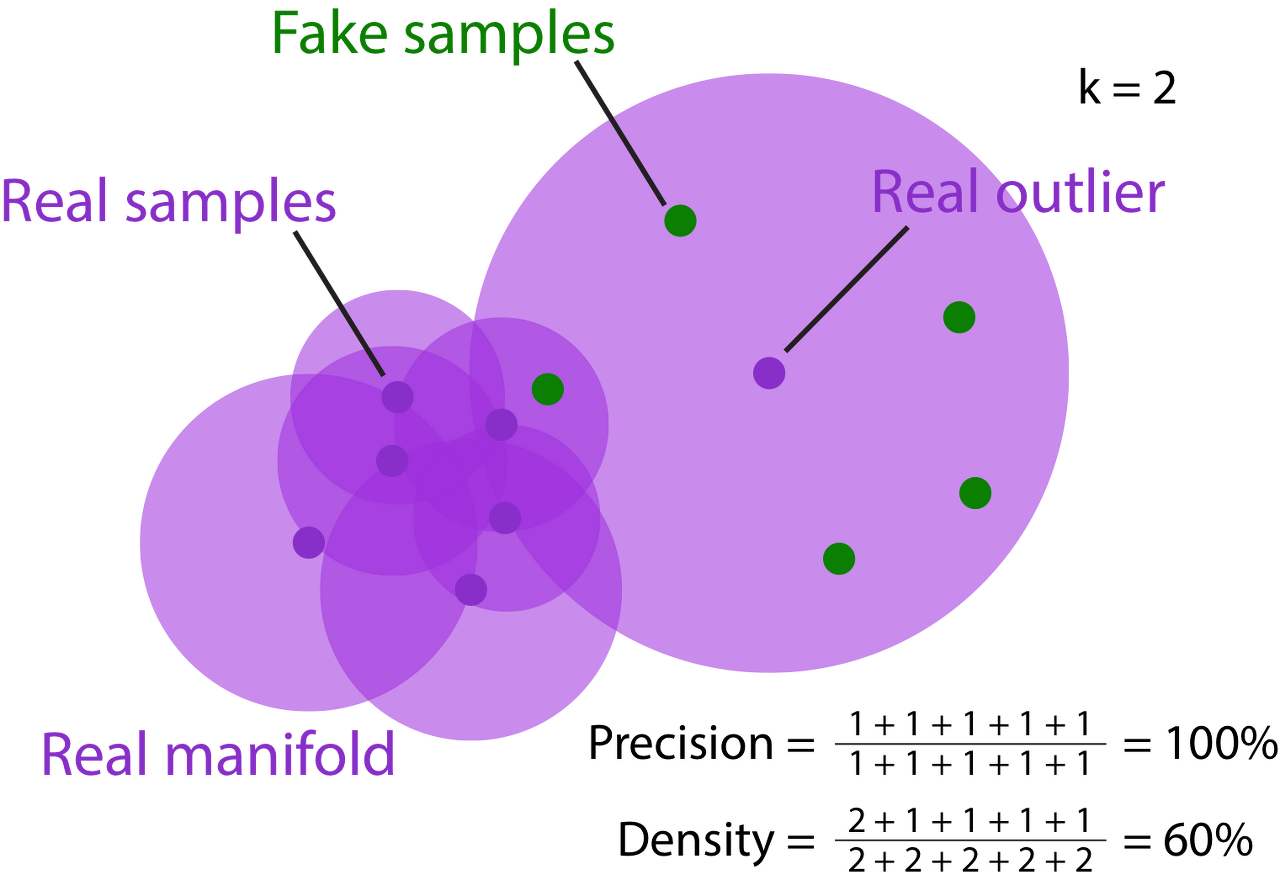
k 값을 조정해서 Manifold를 만든다. 중심점에서 나한테 가장 가까운 거까지만 거리를 r로 해서 ball을 만든다. ball을 union해서 manifold를 만든다.
Precision은 Real Manifold에서 fake가 얼마나 들어가느냐를 계산한다.
= (fakes in real manifold) / total fakes
fake가 manifold 안에 위치할 수록 더욱 fidelity = realistic한 아이들이다. 라고 볼 수 있다.
Recall은 Fake Manifold에서 real이 얼마나 들어가느냐를 계산한다.
= (reals in fake manifold) / total reals
real이 fake manifold 안에 위치할 수록 더욱 diverse가 상당히 괜찮아진다.
그러나 한계가 있다.
(1) Outlier에 민감하다.
Evaluation은 원래 Outlier에 민감한데, 이 평가 모델은 outlier가 단 하나만 있어도 결과가 매우 달라진다.
(2) Real == Fake일 때 1이 되지 않는다.
(3) hyperparameter에 따라 매우 민감하다.
-> 샘플의 갯수가 많아질 수록 메트릭의 precision_recall이 떨어진다.
-> embedding하는 feature dimension이 많아질 수록 떨어진다.
-> high dimension으로 갈수록 서로 떨어져있는 점들이 많아지기 때문에 점들이 dimension이 높아지면서 분리가 더 잘 되기 때문이다. 31:33
-> k값을 키울 수록 precision recall 값은 커진다. (당장 k값은 휴리스틱하게 찝는다)
-> 어떤 distribution type에서 하느냐에 따라서 값도 바뀐다.
이러한 불안정성 때문에 evaluation으로 쓰기에는 문제가 많다.
(4) Mode-dropping에 둔감하다.
(MNIST 데이터에 대해서 0 ~ 9까지의 숫자 중 0~ 8까지의 숫자만 뽑아내더라도 9를 뽑아내지 않았다, 즉, 모드가 하나 없어진 거에 대해서 알아내지 못한다.)
Real Distribution시 모드가 4개있다고 가정할 때 Fake Distribution의 경우,
Sequential dropping을 하면 Recall은 모드의 감소를 인식한다.
그러나 Simultaneous dropping이 되면 하나의 데이터라도 한 모드에 있다면 모드가 있다고 감지하기 때문에 recall이 모드 감소를 인식하지 못한다.
(5) 생성모델이 Fake sample을 만들어내면서 매번 manifold를 만들어내는 것은 Computed 오버헤딩이 크다.
중간중간에 확인하고 싶으면 manifold를 매번 만들어내야한다. 왜냐하면 generator가 매번 학습하면서 바뀌기 때문이다. fake sample에 manifold를 만드는 것은 좀 문제가 있다. 많은 아웃라이어가 페이크 샘플에 주로 생기는데, 모든 모델 혹은 에폭마다 매니폴드를 만들어줘야 하므로 오버헤드가 생긴다.
해결점
(1) Density를 이용하여 manifold를 만든다.
(기존)
precision을 이용하여 manifold를 형성.
-> union (합집합)
(해결)
density를 이용하여 manifold를 형성
-> superposition (교집합 = Realistic 샘플이 더 많은 쪽에 더 많은 가중치를 준다. Outlier에 더 강건해짐. Fidelity)
(2) Manifold 생성을 Fake sample에서 real sample로 한정한다.
(기존)
Recall은 Fake sample에서 manifold를 만들어낸다.
(해결)
Real sample에서 manifold를 만들어내자. Coverage라는 특성을 쓴다.
- 이점 : 원래 real에서 outlier가 있는 것 보다, fake에서 outlier가 있는 경우가 더 많다. 그러므로, real에서 manifold를 만들면 더 결과값이 stable하게 나올 수 있다.
- 컴퓨팅 적으로 오버헤드를 방지할 수 있다. 왜냐하면 fake와는 달리 real data는 갱신을 하는 등의 변화가 없기 때문이다. 그러므로 오로지 한번만 manifold를 생성한다.
precision과 recall 은 휴리스틱하다보니 analytical한 behavior을 분석할 수 있는 방법이 없다.
M이나 N 갯수도 그냥 실험적으로 진행을 해보면서 정하는 거였다.
그러나, Density와 Coverage는 수식으로 왜 이런지 설명할 수 있다.
Real과 Fake의 distribution이 같을 때를 가정하고,
Density의 기댓값은 무조건 1이다!
Coverage의 기댓값은 동영상(40:52)와 같은 수식으로 나오는데, 데이터의 수, k의 값에 따라서 Coverage의 기댓값이 1에서 약간 줄어드는 형태로 된다. (왜 이러한 수식이 나왔는지는 아직 이해 하지 않았다)
1 - 2^(-k)
충분히 큰 M과 N, 그리고 k에 따라서 1에 가까워져야 한다.
차원과 분포 방식에 따라서 독립적이어야 하는데, precision과 recall의 기댓값은 그런 평가방식이 없다.
Coverage의 기댓값을 정할 때, 특정 p값을 선정하여 이것보다는 높게 나와야 한다라는 기준치를 선정할 수 있다. (0.95) 그럼 이거에 따라서, M과 N 그리고 k 값을 유추할 수 있다. 그러므로 이론적인 분석이 가능해진다.
샘플링 차이에 의해 약간에 분포의 요동은 있겠지만, distribution에 독립적으로 작용한다. (= distribution에 영향을 받지 않는다)
D&C(Density and Coverage)는 Recall에 비해 Mode-Collapse를 매우 잘 찾아낸다.
특히, Simultaneous dropping 상태에서도 Coverage는 Smooth하게 표현해준다. (Sensitive 하다) (왜일까...)
Random Embedding
Embedding (이미지에 Tie 되어 있다.)
-> 이미지넷 같이 생긴 이미지 뿐만 아니라 다른 generative한 어플리케이션이 많은데, 우리가 이미지넷만 쓸거는 아니지 않을까
Random Embedding을 사용하자.
이미지넷에서도 pretained 된 embedding을 사용해서 mnist에 적용해보면 p&r, d&c도 낮게 나온다. embedding space가 문제가 있어서 그런거다. 근데 눈으로 봤을 때는 괜찮아 보임...
완전한 random embedding을 적용해보았다. weight가 fix 된 random을 주기. 즉, cnn이 가진 구조가 주는 random embedding인 셈이다. 이러면 p&r, d&c도 높게 나온다.
CNN이 적용 가능한 Random embedding을 적용하게 되면 이미지 뿐 아니라 다른 도메인에서도 inductive bias를 넣지않고도 평가가 공평하게 가능하다. 그러므로 general한 어플리케이션이 가능하다.
(대신에 학습데이터가 많고 Feature space를 좋게 학습이 가능한 classfication이면 그 space에서 embedding을 만들어서 그 embedding을 보내서 계산한다. 대신,,, 모든 도메인의 데이터가 이미지넷처럼 많이 있지도 않고 feature가 다양하지도 않기 때문에 random embedding을 제안한 것이다.)
contrastive learning / self supervised learning 등이 많이 나오고 있는디... random embedding을 쓰지 않더라도 이런 embedding에서 쓰는 것도 의미가 있을 것 이다.
Summary
-> Fidelity와 Diversity Metrics는 평가 수단으로서 매우 유용하다.
-> Precision과 Recall은 문제점을 가지고 있다.
-> Density와 Coverage는 이러한 문제점을 해결할 수 있다.
-> CNN 구조의 Random Embedding을 적용하게 되면 좀더 General한 어플리케이션이 가능하다.
Outlier가 있어도 evaluation 모델이 영향을 받지 않게 하도록 만드는 것이다!
단점 :
(1) 하나의 메트릭이 아닌 두 가지(Fidelity & Diversity)로 분리가 되어 있는데, 두 가지의 상관관계를 따질 수가 없기 때문에... FID처럼 모델을 순서 세우기가 쉽지 않다. 그러므로 FID가 보조적으로 들어가야한다. 보조적인 역할로, 좀더 모델의 비교가 가능하긴 하다.
(2) Embedding Space가 완벽한 대안은 아니다.
질문
출현 키워드 : Deep Image Prior
random weight으로 initial해서 walking을 어케 하는걸까?
deep image prior walk?
cnn의 구조 자체가 주는 structure한 prior가 있다?
cnn의 구조를 정하는 순간 표현할 수 있는 함수 공간이 딱 정해진다. 모든 함수를 표현할 수 있는 건 아니니까.
근데 그 함수공간이 꽤나 좋은 녀석들이라서 noise를 피팅하는 함수공간을 찾으려고 해도 그 함수를 찾을 수 없어... 그 녀석이 의미하는 것은 뭐냐? 이게 deep image prior이다
-> cnn의 구조자체가 inductive prior가 있다는 것임. infinite prior?(인피니시 프라이어?)
구조는 휴리스틱하지만 경험적인 구조를 사용한다. weight은 learned prior는 아니더라도 하나의 cnn structure가 주는 bias가 있다는 것임. 추측이다.
피쳐공간을 의미있는 공간으로 보내는 것?
유클리디안 매트릭 디스턴스가 의미있는 피쳐공간으로 보낸다는 것은 거리가 의미를 갖는 공간이 되는 것이다.
random embedding은 어떤 공간으로 projection 했는지는 모르지만 거리가 대충은 의미가 갖는 듯 하다.
아마 Compressed Sensing (압축센싱) 과 연관이 있을 것이다.
cnn 구조가 아닌 dense layer로는 의미가 없다. (사실 나(필자)는 dense layer를 모른다 = 까먹었다)
***현재 발표자님이 진행하고 있는 연구 내용***
medical image reconstruction에 주로 사용중이다.
measurement로 projection하는 시스템...
denoising diffusion model을 가지고 generative하는 것도 있다.
normalizing flow도 있다. noise을 먼저 만든다음에 invert 하는 함수를 만들면 생성이 잘되기도 한다.
Generative Model과 Inverse Problems
어떻게 하면 GAN을 Inverse Problem에 어케 풀어볼까?
Cryo-EM : 분자구조 영상을 어케하면 다 예측하고 분석하고 reconstruction할까? 이걸 gan으로 만들어서 연구
Dynamic MRI : MRI는 한줄한줄 찍기 때문에 너무 느리고 한장을 얻기가 너무 힘들다. 특히 움직이는 것을 만든다는게... 특히 태아의 심장은 어케 찍나? 이거를 deep image prior 등으로 문제를 풀어보자~ 장점 = unsupervised learning이라서 기존의 최적화 방식이 아니라서 23db, 4db recon 방식이라 좋다?
Reference
- 1시간만에 GAN(Generative Adversarial Network) 완전 정복하기 : https://youtu.be/odpjk7_tGY0
- [머신러닝] 다중 분류 모델 성능 측정 (accuracy, f1 score, precision, recall on multiclass classification) :https://youtu.be/8DbC39cvvis
- GAN 성능의 정량적 평가 방법 - Python, Deep Learning : https://youtu.be/19An2T4utEM
- KL Divergence, 순서가 중요할까요? : https://www.youtube.com/watch?v=c5nTnvGHG4E
- 생성모델, 어떻게 평가해야 할까? (EPFL 유재준) : www.youtube.com/watch?v=onssrAFErsM&t=6s
- 정보 이론: Information Theory 1편 : brunch.co.kr/@chris-song/68
- 머신러닝 구글 디벨로퍼 : developers.google.com/machine-learning/crash-course/embeddings/video-lecture?hl=ko
- Bayesian Deep Learning: Introduction : taeoh-kim.github.io/blog/bayesian1/
Inception Score & Frechet Inception Distance : cyc1am3n.github.io/2020/03/01/is_fid.html
'알아본 것' 카테고리의 다른 글
| GAN을 이해 하기까지의 과정 (0) | 2021.02.05 |
|---|---|
| Bayesian Theorem : Likelihood, Prior, MAP (0) | 2021.01.15 |
| 유튜브 보면서...Predictive Uncertainty of Deep Models 키워드 정리 (정리중) (0) | 2021.01.03 |

