무한한 심해 탐험
Bayesian Theorem : Likelihood, Prior, MAP 본문
기존의 통계학, 전통적인 통계 관점에서는 '빈도주의(Frequentism)'를 기반으로 엄격하게 확률 공간을 정의하고 계산을 통해 파생되는 빈도수를 기반으로 하여 확률을 계산하였다.
ex. 가령, 동전 100개 중 앞면이 나올 확률을 구하기 위해서는 실제로 동전을 100번 던진 다음에 앞면이 나오는 횟수를 빈도를 통하여 얻는다.
이러한 빈도는 일어나지 않은 일에 대한 확률. 즉 불확실성이 연관되어 있고, 빈도 확률 방법으로는 측정이 어려운 사건들의 확률들에 대하여 신뢰할만한 값을 얻기 어렵다는 한계점이 존재했다.
베이지안 관점의 통계학에서는 이러한 반복할 수 없는 사건들, 일어나지 않은 일에 대한 확률을 추정하기 위해 사건과 관련있는 다른 여러 확률을 이용하여 새롭게 일어날 사건을 추정하는 것이 목표이다.
베이즈 이론은 사전확률 p(A)와 우도확률 p(B|A)를 안다면, 사후확률 p(A|B)를 알 수 있다는 것이다. 또한, 베이즈 이론에서 사건들은 모두 배반사건일 때 이용할 수 있다.
여기서 잠깐 조건부 확률이 나오는데, 조건부확률의 의의는 Sample Space를 줄이는 것이다. 과거의 경험, 알고있는 정보로 범위를 축소하여 관심 있는 사건의 확률에 대해 추정하는 것이다. 베이즈이론에서는 이 조건부확률을 이용함으로써 sample space를 줄여서 사건의 확률을 추정해가는 것이다.

H : Hypothesis의 약자. 가설 혹은 '어떤 사건이 발생했다는 주장' 즉 원인이 된다.
E : Evidence의 약자. '새로운 정보, 혹은 데이터'
P(H) : 어떤 사건이 발생했다는 주장에 관한 신뢰도 (사전확률 Prior)
P(E|H) : H가 발생했다는 조건하에 E가 발생할 확률. (우도확률 Likelihood)
P(H|E) : 새로운 정보를 받은 후 갱신된 신뢰도 (사후확률 Posterior)
새로운 정보 P(E)를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방법이다.
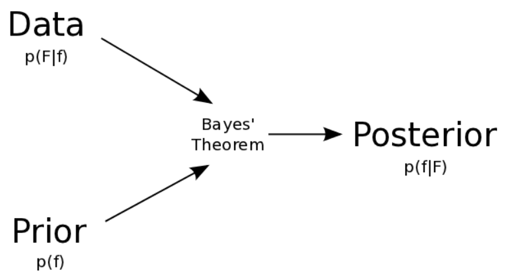


사후확률과 사전확률은 비례관계에 있다.
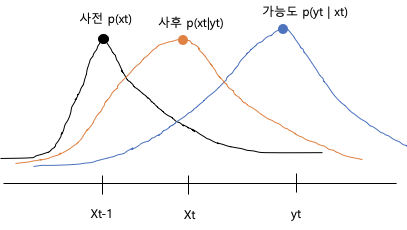
기호가 좀 깔끔하지는 않지만... 위의 수식과 그림을 비교했을 때, xt를 실제값, yt를 예측값이라고 보았을 때, 실제 xt-1에서 나온 값에서 yt를 예측하고, 이 예측한 값 yt와 xt-1를 곱함으로써 yt값이 나왔을 때의 xt 값을 갱신한다. 이것은 실제 자동차의 위치를 GPS로 측정한 값과 실제 자동차의 위치값을 비교해나가며 그 차이를 줄여나가는 방식에 쓰인다.
앞서서 계산한 사후확률이 다시 사전확률로 주어지고, 이를 이용하여 한번 더 갱신한 사후확률을 계산할 수 있다. 이로써, 계산하여 얻은 사전확률에 근거를 기반으로 하여 확률을 갱신해주는 것이다.
확률(Probability)
- 모수로부터 다음과 같이 관찰될 확률은?
우도 (Likelihood)
- 현상에 대해 가장 가능성이 높은(우도가 높은) 모수는?
우도는 나타난 결과에 따라 여러 가능한 가설들을 평가할 수 있는 측도(Measure)가 된다.
확률분포함수의 y값, 일어날 가능성이 높은 사건이 된다.
최대우도법 (Maximum Likelihood Estimation) - MLE
- 주어진 현상을 가지고 이 현상이 추출될 가능성을 가장 높게 하는 모수를 거꾸로 추적하는 방법
모수적인 데이터 밀도 추정 방법으로써, 확률밀도함수 p(x|theta)에서 관측된 표본 데이터 집합을 x라고 할 때 이 표본들 x로부터 파라미터 theta를 추정하는 방법이다.
최대우도법의 목표
- 주어진 파라메터를 기반으로 데이터의 가능도를 최대화 한다.
- (log) likelihood의 음수를 최소화 한다.
사건의 발생확률을 최대로 높이는 모델 변수를 찾는 것이다.
확률분포를 최대로 할 수 있는 theta값을 찾는 것이 최대우도법이다.
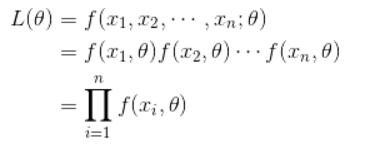

나온 데이터들(x)들이 어떻게 나왔는지에 대한 가능도에 대한 Likelihood function 분포는 매우 다양하지만, 가장 높은 가능도를 가질 수 있는 최대값의 지점이 있다. 이것이 최대 우도값이다.
측정된 관측자료들을 토대로 모분포의 평균과 분산을 추정해나간다.
정규분포에서의 모평균 추정 공식
$ μ = \cfrac{1}{n} \times \sum_{i=1}^{n}x_i $
정규분포에서의 모분산 추정 공식
$ \sigma ^2 =\cfrac{1}{n} \times \sum_{i=1}^{n}{(x_i - \mu )^2} $
P(x|theta) = Likelihood function에 Log를 취해준다.
-> 왜?
Log-likelihood function을 취해주는 이유는, 계산이 쉽기도 하고(곱하기는 합이 되기 때문), 최대값을 찾기 쉽기 때문이다.
L(theta|x)의 최댓값을 찾아주면 된다.
미분(혹은 편미분)을 이용하여 0이 되는 부분이 최댓값이 되는 부분이므로 미분한 값이 (기울기가) 0이 되는 theta 값을 찾을 수 있다.
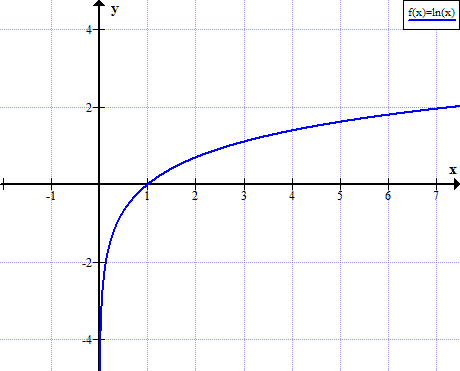
* Gaussian Distribution의 경우, 다음과 같은 최대 가능도가 나올 수 있는 w값을 추정하는 공식이다.
Gaussian Distribution은 정규분포 형태를 띄기 때문에 정규분포의 확률밀도함수를 가지고 있다. 여기서, 로그를 취하면 시그마 안에 값을 키울 수록 최대값이 나오게 되고 이는 즉, 음수를 제거한다면 (yi - fw(xi))^2)값을 최소화 하는 것과 동치이다.
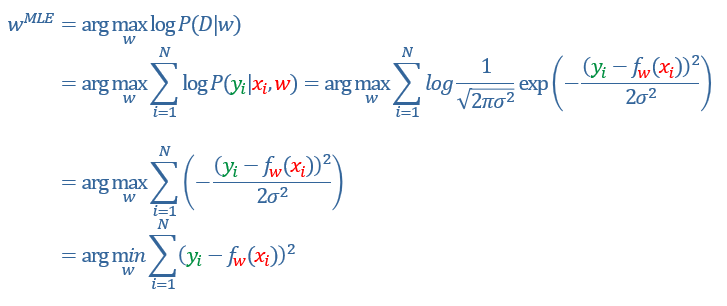
MLE의 한계점
관찰값에만 의존하여 Outlier에 민감.
- Observation에 전적으로 의존한다. 편향된 데이터에 영향을 받을 수 있다.
MAP (Maximum a Posteriori Estimation)

L : likelihood로서 데이터로부터 계산한 것이다.
f(theta) -> prior probability로서, 파라메터 자체의 확률이다. = 사전지식이다.
- prior = f(theta)라는 강력한 가설을 추가함으로써 MLE의 데이터 의존 문제를 해결한다.
(사전분포에 영향을 받는데, 보통은 uniform distribution 혹은 gaussian distribution을 이용한다.)
* 데이터의 양이 충분히 많아지면, prior 값의 영향이 거의 없어진다는 연구결과가 있다.
MLE는 Likelihood를 Maximize하고, MAP는 Posterior을 Maximize하여 추정치를 얻는 방법론이다.
Reference
- MLE vs MAP : (Maximum Likelihood or Maximum a Posteriori) niceguy1575.tistory.com/entry/MLE-vs-MAP-Maximum-Likelihood-or-Maximum-a-Posteriori
- Bayesian 모수 추정 : namyoungkim.github.io/statistics/2017/09/18/probability/
- 베이즈 정리를 이해하는 가장 쉬운 방법 : www.youtube.com/watch?v=Y4ecU7NkiEI
- 베이지안 추론 이론 : sumniya.tistory.com/29
- MLE와 MAP에 관하여 : gaussian37.github.io/ml-concept-mlemap/
- 베이지안 이론 (Bayesian theory) : bioinformaticsandme.tistory.com/47
- 최대우도법(MLE) : angeloyeo.github.io/2020/07/17/MLE.html
'알아본 것' 카테고리의 다른 글
| GAN을 이해 하기까지의 과정 (0) | 2021.02.05 |
|---|---|
| [21년 1월 2주차] 생성 모델, 어떻게 평가해야 할까? (EPFL 유재준) (0) | 2021.01.08 |
| 유튜브 보면서...Predictive Uncertainty of Deep Models 키워드 정리 (정리중) (0) | 2021.01.03 |

